Cómo Calcular Correctamente el Vector del Viento en Aplicaciones de Ingeniería

1. Introducción

En múltiples aplicaciones de ingeniería como el análisis del rango de chorros de agua o espuma de agua, estudios de dispersión, ventilación industrial y protección contra incendios, es esencial interpretar correctamente la dirección del viento y transformarla en un vector físico que pueda utilizarse en cálculos.

2. Convención de Dirección del Viento

La dirección del viento siempre se define como la dirección DESDE DONDE viene el viento, y no hacia donde se dirige.

Ejemplos:

· Viento del norte (N): viene del norte y sopla hacia el sur.

· Viento del este (E): viene del este y sopla hacia el oeste.

· Viento del ESTE: viene del este-noreste y sopla hacia el oeste-suroeste.

3. Sistema de Referencia y Azimut

El sistema de azimut se utiliza con un origen norte (0°) y una dirección en sentido horario.

N: 0°
NNE: 22.5°
NE: 45°
ENE: 67.5°
E: 90°
ESE: 112.5°
SE: 135°
SSE: 157.5°
S: 180°
SSO: 202.5°
SO: 225°
OSO: 247.5°
O: 270°
ONO: 292.5°
NO: 315°
NNO: 337.5°

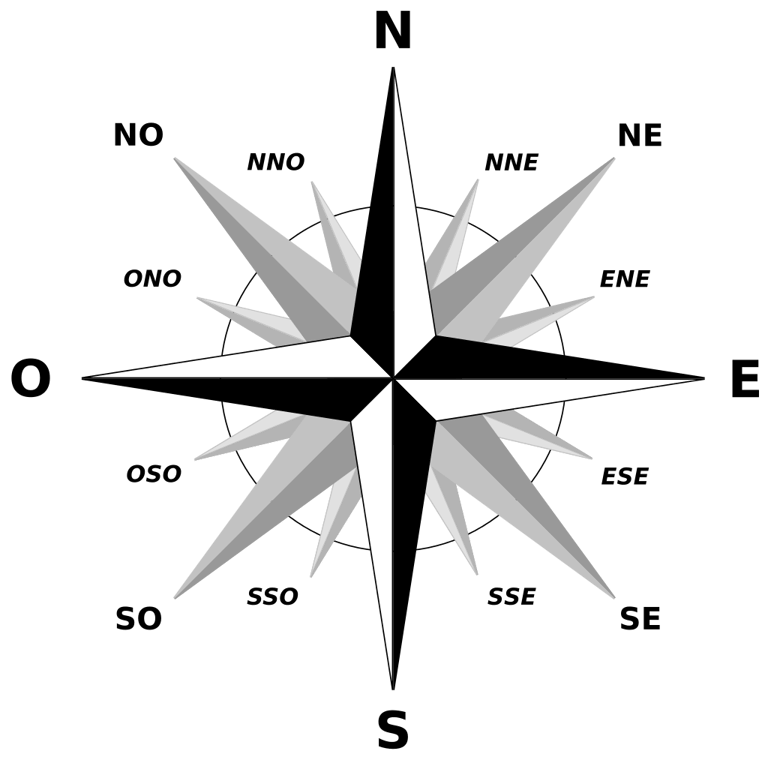
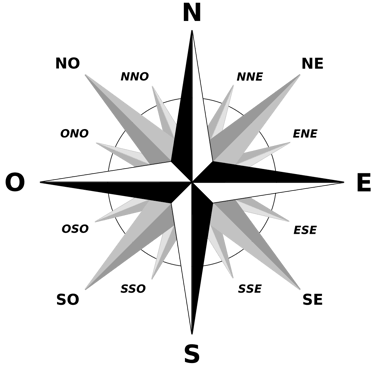
4. Dirección del Viento vs Vector del viento

El vector viento representa la dirección real en la que se mueve el aire y se obtiene invirtiendo la dirección meteorológica en 180°.

5. Cálculo del Angulo del Vector del Viento

Para θ_direction + 180° < 360°
θ_w = θ_direction + 180°

Para θ_direction + 180° ≥ 360°
θ_w = θ_direction − 180°

6. Ejemplos Prácticos

Viento ENE: Dirección: 67,5° → Vector del viento: 247,5°

Viento SSO: Dirección: 202,5° → Vector del viento: 22,5°

7. Uso en Cálculos de Ingeniería

El vector viento se utiliza para calcular las componentes paralelas y perpendiculares del viento respecto a un eje de interés.

V∥ = V_w · cos(Δθ)

V⊥ = V_w · sen(Δθ)

Donde Δθ = θ_w – θ_j

θ_j = Azimut del monitor

8. Recomendaciones finales

Siempre convertir la dirección meteorológica del viento en vector de viento antes de realizar los cálculos.