Cálculo del Alcance y Trayectoria de Chorros en Monitores de Agua y Agua-Espuma – Parte I

1. Introducción

En los sistemas de combate de incendios mediante monitores de agua o agua-espuma, el alcance del chorro es un parámetro crítico para garantizar una cobertura efectiva del área a proteger. Sin embargo, en la práctica, el alcance real del chorro no depende únicamente del valor indicado por el fabricante, sino también de factores geométricos, ambientales y operativos propios de cada instalación.

En proyectos industriales, terminales de hidrocarburos y plantas de proceso, es habitual que los monitores:

• estén instalados a cierta altura sobre el terreno,

• deban disparar por encima de diques, muros o estructuras,

• operen bajo condiciones de viento variable, y

• deban cubrir un área localizada a una distancia específica, no necesariamente igual al alcance nominal.

Este artículo presenta una metodología ingenieril completa, basada en principios físicos clásicos y modelos semiempíricos, que permite:

• utilizar correctamente la información suministrada por el fabricante,

• calcular la ecuación real de la trayectoria del chorro,

• verificar interferencias con obstáculos inferiores y superiores,

• evaluar el efecto del viento en distintas direcciones, y

• determinar el ángulo de inclinación requerido cuando se conoce la distancia al área a proteger.

El presente artículo se enfoca en el desarrollo del marco teórico y las ecuaciones fundamentales necesarias para el análisis del alcance y la trayectoria de chorros en monitores de agua y agua-espuma.

En un segundo artículo, se presentarán ejemplos prácticos de cálculo, aplicados a configuraciones reales de monitores, con el objetivo de ilustrar la aplicación directa de la metodología aquí desarrollada.

2. Información Básica del Fabricante

Los fabricantes de monitores suelen suministrar los siguientes datos básicos:

• Caudal nominal Q

• Presión de operación P

• Alcance efectivo R_fab para un ángulo específico.

• Angulo α_fab utilizado por el monitor para el alcance efectivo.

Estos valores se determinan bajo condiciones controladas, sin viento y con la boquilla ubicada a nivel del suelo. En esta metodología, el alcance del fabricante se utiliza para calibrar la velocidad inicial del chorro.

El alcance especificado por el fabricante se basa en condiciones óptimas de prueba y, por sí solo, no garantiza una cobertura efectiva en condiciones reales de instalación.

3. Velocidad Inicial del Chorro

La velocidad inicial del chorro se estima a partir del caudal y del diámetro de la boquilla:1. Introduction

v₀ = Q / A₀

donde:

A₀ = π · d₀² / 4

En la práctica, cuando el fabricante proporciona directamente el alcance R_fab para un ángulo α_fab, se puede obtener v₀ resolviendo la ecuación balística inversa:

R_fab = (v₀² / g) · sin(2α_fab)

dondee:

v₀ = √(R_fab · g / sin(2α_fab))

4. Modelo Balístico del Chorro Sin Viento

El chorro se modela como un proyectil sometido únicamente a la aceleración de la gravedad.

En el presente modelo se adopta una aproximación balística simplificada. Este modelo no considera efectos aerodinámicos complejos como atomización, pérdida de coherencia del chorro ni variaciones del coeficiente de arrastre (Cd), por lo que es aplicable a análisis geométricos, comparativos y de verificación preliminar de alcance y trayectoria.

4.1 Trayectoria

La trayectoria viene dada por:

y(x) = h₀ + x · tan(α) − (g · x²) / (2 · v₀² · cos²(α))

Donde x es la distancia horizontal medida desde el monitor, y, y(x) es la altura del chorro respecto al nivel de referencia.

Esta ecuación permite calcular la altura del chorro en cualquier punto x, y verificar interferencias con obstáculos.

4.2 Altura Máxima del Chorro

La altura máxima se alcanza cuando la velocidad vertical es cero. Su expresión es:

y_max = h₀ + (v₀ · sin(α))² / (2 · g)

4.3 Alcance Horizontal Sin Viento

Cuando la boquilla se encuentra a una altura h₀ distinta de cero respecto al nivel de referencia, el alcance real se obtiene resolviendo y(x) = 0. El alcance R se calcula como:

R = v₀ · cos(α) · t_f

R = (v₀·cos(α)/g) · [ v₀·sin(α) + √( (v₀·sin(α))² + 2·g·h₀ ) ]

Siendo el tiempo de vuelo:

t_f = [ v₀ · sin(α) + √( (v₀ · sin(α))² + 2 · g · h₀ ) ] / g

Si h₀ = 0, la ecuación del alcance queda de la siguiente manera:

R = 2 · v₀² · sin(α) · cos(α) /g

R = v₀² · sin(2α) / g

4.4 Distancia al Punto de Altura Máxima del Chorro

La distancia horizontal x_max desde la boquilla del monitor hasta ese punto de altura máxima depende únicamente del ángulo de inclinación α y de la velocidad del chorro v₀.

Esta distancia se calcula como:

x_max = (v₀² · sin(2α)) / (2 · g)

4.5 Verificación de Obstáculos

Para verificar obstáculos se evalúa la altura del chorro en la posición del obstáculo.

• Muros o diques:
  El chorro debe cumplir y(x_muro) > h_muro, considerando además la profundidad del muro.

• Techos o estructuras superiores:
  Debe cumplirse y(x_techo) < h_techo para evitar impacto.

4.6 Cálculo del Angulo de Inclinación Requerido

Cuando se conoce la distancia horizontal D al área a proteger, el ángulo del monitor puede determinarse resolviendo la ecuación de trayectoria:

0 = h₀ + D · tan(α) − (g · D²) / (2 · v₀² · cos²(α))

Esta ecuación tiene dos soluciones y puede resolverse de forma iterativa o mediante métodos numéricos.

Otra forma de la ecuación anterior se obtienes de la siguiente manera:

Sustituyendo 1/ cos²(α) = tan²(α) + 1

0 = h₀ - (g · D²) / (2 · v₀²) + D · tan(α) - (g · D² · tan²(α)) / (2 · v₀²)

Haciendo T = tan(α) tenemos

T²· (g · D) / (2 · v₀²) – T · D + (g · D²) / (2 · v₀²) - h₀ = 0

Esta es una ecuación cuadrática con los siguientes términos:

A = (g · D) / (2 · v₀²)

B = -D.

C = (g · D²) / (2 · v₀²) - h₀

T = [ −B ± √(B² − 4 · A · C) ] / (2 · A);

α = arctan(T)

El ángulo seleccionado depende de la aplicación;

• Para aplicaciones que no requieren mucha altura de chorro, ej., suministro de espuma o agua en área de bombas o en áreas que están bajo techo se recomienda seleccionar el ángulo menor.

• Para aplicaciones que requieren una altura mayor ej., inyección de espuma en tanques de almacenamiento se recomienda seleccionar el ángulo mayor.

5. Introducción del Efecto del Viento

El viento se descompone en componentes paralela y perpendicular al eje del chorro:

V∥ = V_w · cos(Δθ)
V⊥ = V_w · sin(Δθ)

Donde:

Δθ = θ_w – θj

θw = Angulo del vector de la dirección del viento

θj = Azimut del monitor

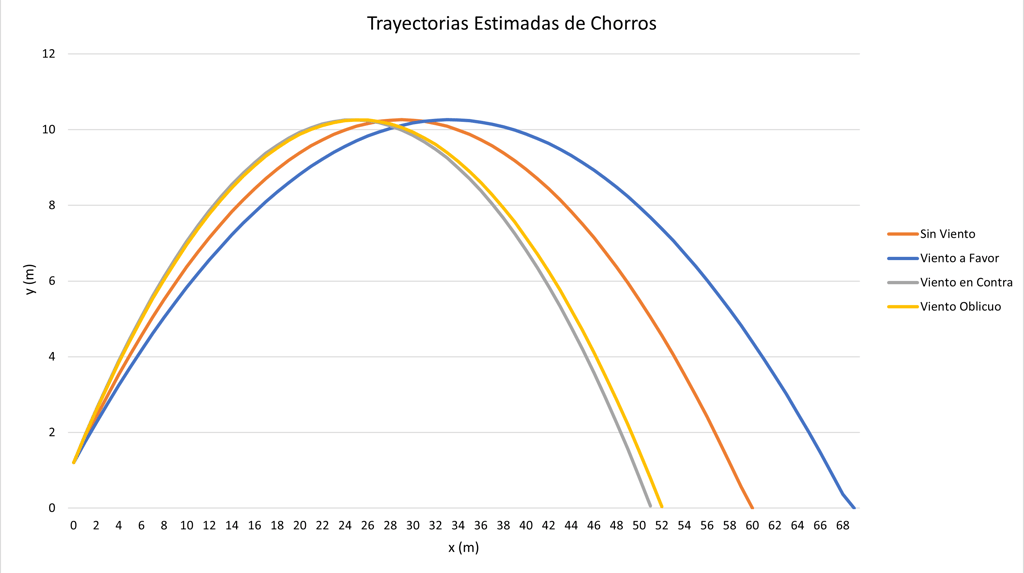
El viento paralelo modifica el alcance efectivo, mientras que el viento lateral o perpendicular introduce una deriva o desviación transversal.

6. Modelo Balístico del Chorro Con Viento

Definiciones geométricas de alcance con viento

Para evitar ambigüedades en la interpretación de los alcances cuando existe viento, se definen los siguientes términos:

R∥ : Alcance longitudinal del chorro en la dirección principal del disparo, considerando únicamente la componente del viento paralela al eje del chorro.

D_z : Deriva o desviación transversal del chorro causada por la componente del viento perpendicular al eje del chorro.

R₃D : Distancia real del punto de impacto en planta, resultante de la combinación vectorial del alcance longitudinal y la deriva lateral, definida como:

R₃D = √(R∥² + D_z²)

Estas definiciones se mantendrán a lo largo del presente capítulo para diferenciar claramente entre alcance longitudinal, desviación lateral y alcance real en planta.

6.1 Velocidad Horizontal Efectiva

v_x,eff = v₀ · cos(α) + V∥

• Si el viento está en contra Vǁ < 0, se reduce el alcance efectivo.

• Si el viento es a favor Vǁ > 0, se incrementa el alcance efectivo.

6.2 Trayectoria con Viento Paralelo

y(x) = h₀ + x · (v₀ · sin(α)) / v_x,eff − g · x² / (2 · v_x,eff²)

6.3 Altura Máxima

y_max = h₀ + (v₀ · sin(α))² / (2 · g)

En este modelo balístico simplificado, la altura máxima del chorro no se ve afectada por la presencia de viento paralelo. Esto se debe a que el viento actúa únicamente sobre la componente horizontal de la velocidad, mientras que el movimiento vertical permanece gobernado exclusivamente por la aceleración de la gravedad. Esta condición constituye una hipótesis del modelo adoptado.

6.4 Alcance con Viento Paralelo

R∥ = v_x,eff · t_f

R∥ = (v₀ · cos(α) + V∥) · [ v₀ · sin(α) + √( (v₀ · sin(α))² + 2 · g · h₀ ) ] / g

Donde t_f es el tiempo de vuelo (no cambia en este modelo simple):

El tiempo de vuelo depende únicamente del movimiento vertical del chorro. Dado que el viento no introduce aceleraciones en la dirección vertical, la duración del vuelo permanece inalterada respecto al caso sin viento, siendo función únicamente de la velocidad vertical inicial y de la altura de la boquilla.

t_f(α) = [v₀ · sin(α) + √((v₀ · sin(α))² + 2 · g · h₀ )] / g

6.5 Distancia al Punto de Altura Máxima del Chorro

Cuando existe viento, la altura máxima del chorro se alcanza en el mismo instante que en condiciones de calma, ya que el movimiento vertical está gobernado únicamente por la gravedad. Sin embargo, la distancia horizontal hasta el punto de altura máxima aumenta o disminuye dependiendo de la componente del viento paralela a la dirección del chorro.

Esta distancia se calcula como:

x_max = v_x,eff · v₀ · sin(α) / g

x_max = (v0 · cos(α) + Vǁ) · v₀ · sin(α) / g

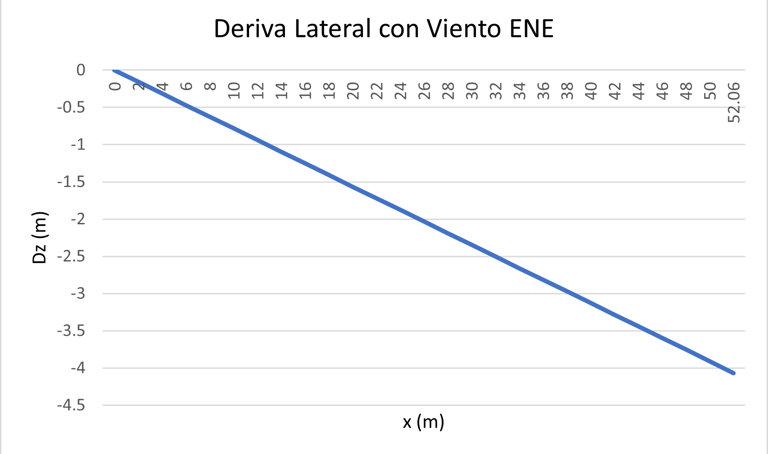
6.6 Deriva o Desviación Lateral

D_z = V⊥ · t_f

6.7 Alcance Real

R₃D = √(R∥² + D_z²)

Si V⊥ = 0 ⇒ D_z = 0 ⇒ R₃D = R∥ , no hay desviación lateral

Angulo de la deriva en planta (desviación del chorro).

b = arctan(Dz/Rǁ)

6.8 Verificación de Obstáculos

Para verificar obstáculos se evalúa la altura del chorro (con viento) en la posición del obstáculo.

• Muros o diques:
  El chorro debe cumplir y(x_muro) > h_muro, considerando además la profundidad del muro.

• Techos o estructuras superiores:
  Debe cumplirse y(x_techo) < h_techo para evitar impacto.

6.9 Cálculo del Angulo α Cuando Conoces la Distancia Objetivo (con viento)

Aquí hay dos casos: (A) objetivo especificado como distancia longitudinal sobre la línea del chorro, o (B) objetivo especificado como distancia en planta (radial) y el viento mete deriva.

Caso A. Si el objetivo está sobre la línea del chorro (se usa D = Rǁ)

Alcance con viento paralelo:

D = (v₀ · cos(α) + V∥) · t_f(α)

t_f(α) = [v₀ · sin(α) + √((v₀ · sin(α))² + 2 · g · h₀ )] / g

D = (v₀ · cos(α) + V∥) · [ v₀ · sin(α) + √( (v₀ · sin(α))² + 2 · g · h₀ ) ] / g

Esta ecuación no se despeja analíticamente de forma limpia (porque α aparece en seno/coseno y dentro de la raíz). En práctica se resuelve con:

• iteración (Newton/Raphson), o

• barrido de α (ej. 5°– 85°) y se elige el que dé D con tolerancia.

Caso B. Si el objetivo está a una distancia radial en planta Dpl y hay deriva

Se exige que el punto de impacto coincida con el objetivo en planta:

D_pl = √( ((v₀ · cos(α) + V∥) · t_f)² + (V⊥ · t_f)² )

Factorizando t_f:

D_pl = t_f · √( (v₀ · cos(α) + V∥)² + V⊥² )

D_pl = [ v₀ · sin(α) + √( (v₀ · sin(α))² + 2 · g · h₀ ) ] / g · √( (v₀ · cos(α) + V∥)² + V⊥² )

También se resuelve por iteración/barrido.

Para ambos casos existen dos soluciones, por lo que el ángulo seleccionado depende de la aplicación requerida;

• Para aplicaciones que no requieren gran altura de chorro, ej., suministro de espuma o agua en área de bombas o en áreas que están bajo techo se puede recomienda seleccionar el ángulo menor.

• Para aplicaciones que requieren una altura mayor ej., inyección de espuma en tanques de almacenamiento se recomienda seleccionar el ángulo mayor..

7. Sumario de Símbolos

Q : Caudal del monitor (m³/s o L/s)
P : Presión de operación del monitor (Pa)
d₀ : Diámetro de la boquilla (m)
h₀ : Altura de la boquilla sobre el nivel de referencia (m)
v₀ : Velocidad inicial del chorro a la salida de la boquilla (m/s)
α : Ángulo de inclinación del monitor respecto a la horizontal (°)
α_fab : Ángulo de inclinación del monitor utilizado por el fabricante para determinar el alcance nominal R_fab​ (°)
x : Distancia horizontal medida desde el monitor (m)
x_max : Distancia horizontal desde el monitor hasta el punto de altura máxima del chorro (m)
y(x) : Altura del chorro a la distancia horizontal x (m)
y_max : Altura máxima del chorro (m)
R : Alcance horizontal del chorro sin considerar efectos del viento (m)
R_fab : Alcance horizontal indicado por el fabricante del monitor (m)
t_f : Tiempo total de vuelo del chorro (s)
V_w : Velocidad del viento (m/s)
V∥ : Componente de la velocidad del viento paralela a la dirección del chorro (m/s)
V⊥ : Componente de la velocidad del viento perpendicular a la dirección del chorro (m/s)
Δθ : Ángulo entre la dirección del viento y la dirección del chorro (°)
θ_w : Ángulo del vector dirección del viento (°)
θ_j : Ángulo azimutal o dirección de descarga del chorro (°)
D_z : Desplazamiento lateral del chorro debido a efectos de viento cruzado (m)
R∥ : Alcance efectivo del chorro considerando viento paralelo a su dirección (m)
g : Aceleración de la gravedad (9,81 m/s²)

8. Conclusiones

El marco teórico presentado permite al lector calcular de forma rigurosa el alcance, la trayectoria y la interacción del chorro con obstáculos y viento.

Este documento constituye la base conceptual y matemática de un segundo blog, en el cual se desarrollarán ejemplos completos de cálculo, aplicados a monitores reales, incorporando datos de fabricante, geometría de instalación, efectos del viento y criterios prácticos de selección del ángulo de descarga.